Midpoint Price Elasticity Of Demand

Learning Objectives

Summate price elasticity using the midpoint method
Differentiate between slope and elasticity

Close-up of three brightly colored rubber bands (blue, gold, and red).

Figure 1. Just how rubberband is information technology?

We take defined cost elasticity of need as the responsiveness of the quantity demanded to a change in the price. We also explained that price elasticity is defined as the percent change in quantity demanded divided past the percent change in price. In this section, y'all will get some practice computing the price elasticity of demand using the midpoint method.

Midpoint Method

To summate elasticity, we will use the average pct change in both quantity and price. This is chosen the midpoint method for elasticity and is represented past the following equations:

[latex]\displaystyle\text{pct modify in quantity}=\frac{Q_2-Q_1}{(Q_2+Q_1)\div{two}}\times{100}[/latex]

[latex]\displaystyle\text{percent change in toll}=\frac{P_2-P_1}{(P_2+P_1)\div{2}}\times{100}[/latex]

The advantage of the midpoint method is that one obtains the aforementioned elasticity betwixt two price points whether there is a price increment or decrease. This is considering the formula uses the same base of operations for both cases.

Practise: Calculating the Price Elasticity of Need

Let'southward summate the elasticity from points B to A and from points G to H, shown in Effigy 2, beneath.

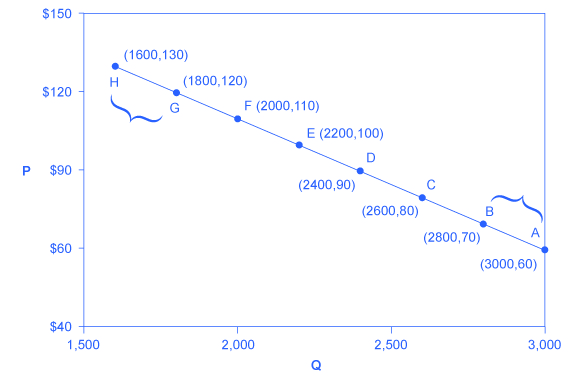
Figure 2. Computing the Price Elasticity of Need. The toll elasticity of demand is calculated as the pct change in quantity divided past the percentage change in price.

Elasticity from Point B to Point A

Step i. We know that [latex]\displaystyle\text{Toll Elasticity of Demand}=\frac{\text{percent alter in quantity}}{\text{percent change in price}}[/latex]

Step two. From the midpoint formula nosotros know that

[latex]\displaystyle\text{percentage modify in quantity}=\frac{Q_2-Q_1}{(Q_2+Q_1)\div{ii}}\times{100}[/latex]

[latex]\displaystyle\text{pct change in price}=\frac{P_2-P_1}{(P_2+P_1)\div{2}}\times{100}[/latex]

Stride 3. We can use the values provided in the effigy (every bit price decreases from $70 at point B to $lx at point A) in each equation:

[latex]\displaystyle\text{percent modify in quantity}=\frac{3,000-2,800}{(3,000+2,800)\div{two}}\times{100}=\frac{200}{two,900}\times{100}=6.9[/latex]

[latex]\displaystyle\text{percent change in price}=\frac{60-seventy}{(60+seventy)\div{two}}\times{100}=\frac{-10}{65}\times{100}=-fifteen.4[/latex]

Step 4. Then, those values can be used to determine the price elasticity of demand:

[latex]\displaystyle\text{Price Elasticity of Demand}=\frac{6.9\text{ percent}}{-15.5\text{ pct}}=-0.45[/latex]

The elasticity of demand between these two points is 0.45, which is an amount smaller than 1. That means that the need in this interval is inelastic.

Retrieve: price elasticities of demand are always negative, since price and quantity demanded always move in reverse directions (on the need curve). As you'll recall, according to the constabulary of demand, price and quantity demanded are inversely related. Past convention, nosotros always talk about elasticities as positive numbers, yet. Then, mathematically, we have the absolute value of the effect. For example, -0.45 would interpreted as 0.45.

This means that, forth the demand bend between points B and A, if the price changes by 1%, the quantity demanded will change by 0.45%. A change in the price will effect in a smaller percentage alter in the quantity demanded. For example, a 10% increase in the price will issue in only a 4.5% decrease in quantity demanded. A 10% subtract in the price will result in only a 4.five% increase in the quantity demanded.

Note also that a larger (negative) number ways need is more elastic, so that if price elasticity of demand were -0.75, the quantity demanded would change by a greater percentage than when the elasticity was -0.45.

Do: Elasticity Of Demand from Point M to Signal H

Calculate the price elasticity of demand using the data in Figure 2 for an increase in cost from G to H. Does the elasticity increase or decrease equally we move up the demand curve?

Step 1. We know that [latex]\displaystyle\text{Price Elasticity of Demand}=\frac{\text{percent change in quantity}}{\text{pct modify in price}}[/latex]

Pace 2. From the midpoint formula we know that

[latex]\displaystyle\text{percent change in quantity}=\frac{Q_2-Q_1}{(Q_2+Q_1)\div{ii}}\times{100}[/latex]

[latex]\displaystyle\text{percent change in price}=\frac{P_2-P_1}{(P_2+P_1)\div{2}}\times{100}[/latex]

Pace iii. We tin use the values provided in the effigy in each equation:

[latex]\displaystyle\text{percent change in quantity}=\frac{1,600-1,800}{(1,600+1,800)\div{2}}\times{100}=\frac{-200}{one,700}\times{100}=-xi.76[/latex]

[latex]\displaystyle\text{percentage change in price}=\frac{130-120}{(130+120)\div{2}}\times{100}=\frac{ten}{125}\times{100}=8.0[/latex]

Step 4. Then, those values can be used to determine the cost elasticity of demand:

[latex]\displaystyle\text{Price Elasticity of Need}=\frac{\text{percent modify in quantity}}{\text{pct change in price}}=\frac{-11.76}{8}=1.47[/latex]

The elasticity of demand from G to H is ane.47. The magnitude of the elasticity has increased (in accented value) every bit we moved up along the demand curve from points A to B. Call back that the elasticity between those two points is 0.45. Demand is inelastic betwixt points A and B and elastic between points Chiliad and H. This shows usa that price elasticity of demand changes at different points along a straight-line need curve.

Let'due south intermission and think well-nigh why the elasticity is different over different parts of the demand curve. When price elasticity of need is greater (as between points Chiliad and H), it means that at that place is a larger impact on demand as price changes. That is, when the price is higher, buyers are more than sensitive to boosted price increases. Logically, that makes sense.

Attempt Information technology

Elasticity Is Non Gradient

It's a common error to misfile the slope of either the supply or demand curve with its elasticity. The slope is the rate of change in units along the curve, or the ascent/run (change in y over the modify in x). For example, in Figure 2 above, for each signal shown on the demand bend, cost drops by $10 and the number of units demanded increases past 200. And so the slope is –10/200 along the entire demand curve, and it doesn't change. The cost elasticity, however, changes along the curve. Elasticity between points B and A was 0.45 and increased to 1.47 between points G and H. Elasticity is the per centum alter—which is a different adding from the slope, and information technology has a different significant.

When we are at the upper stop of a demand bend, where cost is loftier and the quantity demanded is low, a small modify in the quantity demanded—even by, say, one unit—is pretty big in percentage terms. A alter in price of, say, a dollar, is going to be much less important in percentage terms than it will be at the bottom of the demand curve. Likewise, at the bottom of the demand curve, that one unit change when the quantity demanded is loftier will be modest as a pct. Then, at ane end of the need curve, where we have a big percent modify in quantity demanded over a pocket-sized percentage change in price, the elasticity value will be high—demand will be relatively rubberband. Fifty-fifty with the same modify in the cost and the same change in the quantity demanded, at the other end of the demand curve the quantity is much higher, and the price is much lower, then the percentage change in quantity demanded is smaller and the percentage change in toll is much college. Meet Figure iii, beneath:

Graph shows a downward sloping demand curve. The region near the top, where price is high and demand is low, is labeled "more elastic"; the region near the bottom, where price is low and demand is high, is labeled "less elastic."

Figure 3. Elasticity changes along the need curve.

At the lesser of the curve nosotros have a pocket-sized numerator over a large denominator, and then the elasticity mensurate will exist much lower, or inelastic. As we move forth the need curve, the values for quantity and price go upwards or downward, depending on which way we are moving, so the percentages for, say, a $1 difference in price or a 1-unit difference in quantity, will change likewise, which means the ratios of those percentages will change, too.

Try Information technology

Try It

These next questions allow you to get equally much practice as yous demand, as you can click the link at the top of the questions ("Try some other version of these questions") to become a new version of the questions. Practice until you lot experience comfy with this concept.


Glossary elasticity: an economics concept that measures the responsiveness of one variable to changes in another variable midpoint method: measures the boilerplate elasticity over some part of the need (or supply) bend more elastic: the calculated elasticity is greater in absolute value, pregnant the quantity response is greater to the same alter in price