Angle For 6 Sided Box

Shape with six sides

"Hexagonal" redirects here. For For the FIFA World Loving cup qualifying tournament in North America, see Hexagonal (CONCACAF).

Regular hexagon
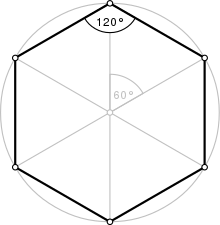A regular hexagon
Type	Regular polygon
Edges and vertices	half-dozen
Schläfli symbol	{6}, t{3}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D6), order 2×half dozen
Internal angle (degrees)	120°
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a hexagon (from Greek ἕξ , hex , meaning "six", and γωνία , gonía , meaning "corner, bending") is a six-sided polygon or 6-gon. The total of the internal angles of whatsoever simple (non-self-intersecting) hexagon is 720°.

Regular hexagon [edit]

A regular hexagon has Schläfli symbol {6}^[ane] and can too exist constructed as a truncated equilateral triangle, t{3}, which alternates ii types of edges.

A step-by-step animation of the construction of a regular hexagon using compass and straightedge, given by Euclid'due south Elements, Book Four, Proposition 15: this is possible every bit 6 ${\displaystyle =}$ two × 3, a product of a power of two and distinct Fermat primes.

When the side length AB is given, drawing a circular arc from betoken A and point B gives the intersection M, the center of the confining circumvolve. Transfer the line segment AB 4 times on the circumscribed circumvolve and connect the corner points.

A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that information technology is both cyclic (has a confining circumvolve) and tangential (has an inscribed circle).

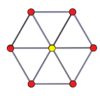
The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals ${\displaystyle {\tfrac {2}{\sqrt {3}}}}$ times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (rotational symmetry of order 6) and six reflection symmetries (six lines of symmetry), making up the dihedral group D₆. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing 1 side with the hexagon is equilateral, and that the regular hexagon can be partitioned into vi equilateral triangles.

Similar squares and equilateral triangles, regular hexagons fit together without any gaps to tile the aeroplane (three hexagons meeting at every vertex), and then are useful for amalgam tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons. Information technology is non usually considered a triambus, although it is equilateral.

Parameters [edit]

The maximal diameter (which corresponds to the long diagonal of the hexagon), D, is twice the maximal radius or circumradius, R, which equals the side length, t. The minimal diameter or the diameter of the inscribed circle (separation of parallel sides, apartment-to-flat distance, short diagonal or pinnacle when resting on a flat base), d, is twice the minimal radius or inradius, r. The maxima and minima are related by the aforementioned factor:

${\displaystyle {\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t}$ and, similarly, ${\displaystyle d={\frac {\sqrt {3}}{2}}D.}$

The area of a regular hexagon

${\displaystyle {\brainstorm{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\[3pt]&={\frac {3{\sqrt {three}}}{viii}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {three}}{ii}}d^{2}\\[3pt]&\approx ii.598R^{2}\approx 3.464r^{ii}\\&\approx 0.6495D^{2}\approx 0.866d^{2}.\end{aligned}}}$

For whatsoever regular polygon, the expanse can as well be expressed in terms of the apothem a and the perimeter p. For the regular hexagon these are given by a = r, and p ${\displaystyle {}=6R=4r{\sqrt {3}}}$ , so

${\displaystyle {\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{ii}}=2r^{2}{\sqrt {3}}\\&\approx 3.464r^{2}.\terminate{aligned}}}$

The regular hexagon fills the fraction ${\displaystyle {\tfrac {three{\sqrt {iii}}}{2\pi }}\approx 0.8270}$ of its confining circle.

If a regular hexagon has successive vertices A, B, C, D, East, F and if P is any point on the circumcircle between B and C, then PE + PF = PA + PB + PC + PD.

It follows from the ratio of circumradius to inradius that the acme-to-width ratio of a regular hexagon is 1:i.1547005; that is, a hexagon with a long diagonal of ane.0000000 will have a altitude of 0.8660254 betwixt parallel sides.

Point in plane [edit]

For an arbitrary signal in the plane of a regular hexagon with circumradius ${\displaystyle R}$ , whose distances to the centroid of the regular hexagon and its six vertices are ${\displaystyle L}$ and ${\displaystyle d_{i}}$ respectively, nosotros have^[2]

${\displaystyle d_{ane}^{2}+d_{4}^{2}=d_{two}^{2}+d_{5}^{2}=d_{3}^{2}+d_{half dozen}^{2}=2\left(R^{two}+L^{2}\right),}$

${\displaystyle d_{one}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{two}+d_{4}^{ii}+d_{6}^{2}=iii\left(R^{2}+L^{ii}\right),}$

${\displaystyle d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{ii}^{4}+d_{4}^{iv}+d_{6}^{iv}=3\left(\left(R^{2}+Fifty^{2}\correct)^{2}+2R^{2}L^{2}\right).}$

If ${\displaystyle d_{i}}$ are the distances from the vertices of a regular hexagon to any point on its circumcircle, then ^[2]

${\displaystyle \left(\sum _{i=1}^{vi}d_{i}^{2}\right)^{2}=four\sum _{i=one}^{6}d_{i}^{four}.}$

Symmetry [edit]

Case hexagons by symmetry
r12 regular i4 d6 isotoxal g6 directed p6 isogonal d2 g2 general parallelogon p2 g3 a1

The six lines of reflection of a regular hexagon, with Dih_vi or r12 symmetry, social club 12.

The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars) Cyclic symmetries in the heart column are labeled equally k for their central gyration orders. Full symmetry of the regular class is r12 and no symmetry is labeled a1.

The regular hexagon has D₆ symmetry. There are xvi subgroups. There are eight up to isomorphism: itself (D₆), 2 dihedral: (D_3, D₂), 4 cyclic: (Z₆, Z_iii, Z_two, Z₁) and the footling (east)

These symmetries limited nine distinct symmetries of a regular hexagon. John Conway labels these by a letter and group order.^[3] r12 is full symmetry, and a1 is no symmetry. p6, an isogonal hexagon synthetic past three mirrors tin can alternate long and short edges, and d6, an isotoxal hexagon constructed with equal edge lengths, simply vertices alternate two different internal angles. These two forms are duals of each other and take half the symmetry gild of the regular hexagon. The i4 forms are regular hexagons flattened or stretched along one symmetry direction. It can be seen as an elongated rhombus, while d2 and p2 tin can exist seen equally horizontally and vertically elongated kites. g2 hexagons, with reverse sides parallel are also called hexagonal parallelogons.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g6 subgroup has no degrees of freedom simply can seen as directed edges.

Hexagons of symmetry g2, i4, and r12, as parallelogons can tessellate the Euclidean plane by translation. Other hexagon shapes can tile the plane with dissimilar orientations.

p6m (*632)	cmm (ii*22)	p2 (2222)	p31m (iii*3)	pmg (22*)		pg (××)
r12	i4	g2	d2	d2	p2	a1
Dih6	Dihii	Z2	Dihi			Zi

A2 and G2 groups [edit]

The six roots of the simple Lie group A2, represented past a Dynkin diagram , are in a regular hexagonal design. The 2 uncomplicated roots have a 120° angle between them.

The 12 roots of the Infrequent Lie group G2, represented by a Dynkin diagram are also in a hexagonal blueprint. The two simple roots of ii lengths take a 150° angle betwixt them.

Dissection [edit]

6-cube project	12 rhomb autopsy

Coxeter states that every zonogon (a 2k-gon whose contrary sides are parallel and of equal length) tin can be dissected into one⁄2 thousand(chiliad − i) parallelograms.^[4] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. This decomposition of a regular hexagon is based on a Petrie polygon projection of a cube, with three of vi square faces. Other parallelogons and projective directions of the cube are dissected inside rectangular cuboids.

Autopsy of hexagons into iii rhombs and parallelograms
second	Rhombs	Parallelograms
	Regular {6}	Hexagonal parallelogons
3D	Square faces		Rectangular faces
	Cube		Rectangular cuboid

Related polygons and tilings [edit]

A regular hexagon has Schläfli symbol {six}. A regular hexagon is a office of the regular hexagonal tiling, {6,3}, with three hexagonal faces around each vertex.

A regular hexagon can besides exist created as a truncated equilateral triangle, with Schläfli symbol t{3}. Seen with two types (colors) of edges, this course only has D₃ symmetry.

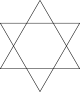
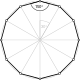
A truncated hexagon, t{vi}, is a dodecagon, {12}, alternating two types (colors) of edges. An alternated hexagon, h{6}, is an equilateral triangle, {3}. A regular hexagon can be stellated with equilateral triangles on its edges, creating a hexagram. A regular hexagon tin can be dissected into six equilateral triangles by calculation a center point. This blueprint repeats within the regular triangular tiling.

A regular hexagon can be extended into a regular dodecagon by adding alternating squares and equilateral triangles around it. This pattern repeats within the rhombitrihexagonal tiling.

Regular {half dozen}	Truncated t{3} = {6}	Hypertruncated triangles			Stellated Star figure 2{3}	Truncated t{half dozen} = {12}	Alternated h{half-dozen} = {3}

Crossed hexagon	A concave hexagon	A self-intersecting hexagon (star polygon)	Extended Fundamental {6} in {12}	A skew hexagon, within cube	Dissected {6}	project octahedron	Complete graph

Self-crossing hexagons [edit]

There are six self-crossing hexagons with the vertex organisation of the regular hexagon:

Self-intersecting hexagons with regular vertices

Dih2			Dih1		Dih3
Figure-eight	Center-flip	Unicursal	Fish-tail	Double-tail	Triple-tail

Hexagonal structures [edit]

From bees' honeycombs to the Giant's Causeway, hexagonal patterns are prevalent in nature due to their efficiency. In a hexagonal filigree each line is equally brusque equally information technology can maybe be if a large expanse is to exist filled with the fewest hexagons. This means that honeycombs crave less wax to construct and proceeds much forcefulness nether compression.

Irregular hexagons with parallel reverse edges are chosen parallelogons and can also tile the plane by translation. In three dimensions, hexagonal prisms with parallel opposite faces are called parallelohedrons and these can tessellate 3-space by translation.

Hexagonal prism tessellations

Form	Hexagonal tiling	Hexagonal prismatic honeycomb
Regular
Parallelogonal

Tesselations by hexagons [edit]

In add-on to the regular hexagon, which determines a unique tessellation of the aeroplane, any irregular hexagon which satisfies the Conway criterion volition tile the airplane.

Hexagon inscribed in a conic section [edit]

Pascal's theorem (also known as the "Hexagrammum Mysticum Theorem") states that if an arbitrary hexagon is inscribed in whatsoever conic section, and pairs of opposite sides are extended until they come across, the iii intersection points volition lie on a direct line, the "Pascal line" of that configuration.

Cyclic hexagon [edit]

The Lemoine hexagon is a cyclic hexagon (one inscribed in a circle) with vertices given by the 6 intersections of the edges of a triangle and the three lines that are parallel to the edges that pass through its symmedian point.

If the successive sides of a cyclic hexagon are a, b, c, d, e, f, then the 3 master diagonals intersect in a single point if and only if ace = bdf .^[v]

If, for each side of a cyclic hexagon, the adjacent sides are extended to their intersection, forming a triangle exterior to the given side, then the segments connecting the circumcenters of contrary triangles are concurrent.^{[half dozen]}

If a hexagon has vertices on the circumcircle of an astute triangle at the half-dozen points (including three triangle vertices) where the extended altitudes of the triangle meet the circumcircle, then the area of the hexagon is twice the area of the triangle.^{[7] : p. 179}

Hexagon tangential to a conic section [edit]

Permit ABCDEF be a hexagon formed past half dozen tangent lines of a conic section. Then Brianchon's theorem states that the three main diagonals AD, Exist, and CF intersect at a single betoken.

In a hexagon that is tangential to a circumvolve and that has consecutive sides a, b, c, d, e, and f,^[viii]

${\displaystyle a+c+e=b+d+f.}$

Equilateral triangles on the sides of an arbitrary hexagon [edit]

Equilateral triangles on the sides of an arbitrary hexagon

If an equilateral triangle is synthetic externally on each side of whatever hexagon, so the midpoints of the segments connecting the centroids of opposite triangles form some other equilateral triangle.^{[9] : Thm. one}

Skew hexagon [edit]

A regular skew hexagon seen as edges (blackness) of a triangular antiprism, symmetry D_3d, [2⁺,6], (2*3), order 12.

A skew hexagon is a skew polygon with half-dozen vertices and edges just not existing on the same plane. The interior of such an hexagon is not mostly defined. A skew zig-zag hexagon has vertices alternate between two parallel planes.

A regular skew hexagon is vertex-transitive with equal edge lengths. In 3 dimensions information technology will be a zig-zag skew hexagon and can be seen in the vertices and side edges of a triangular antiprism with the same D_3d, [2⁺,6] symmetry, order 12.

The cube and octahedron (same as triangular antiprism) have regular skew hexagons as petrie polygons.

Skew hexagons on 3-fold axes

Cube	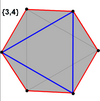Octahedron

Petrie polygons [edit]

The regular skew hexagon is the Petrie polygon for these higher dimensional regular, uniform and dual polyhedra and polytopes, shown in these skew orthogonal projections:

4D		5D
iii-3 duoprism	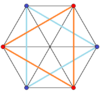three-iii duopyramid	5-simplex

Convex equilateral hexagon [edit]

A principal diagonal of a hexagon is a diagonal which divides the hexagon into quadrilaterals. In any convex equilateral hexagon (one with all sides equal) with common side a, there exists^{[10] : p.184, #286.iii} a principal diagonal d ₁ such that

${\displaystyle {\frac {d_{one}}{a}}\leq two}$

and a master diagonal d _ii such that

${\displaystyle {\frac {d_{2}}{a}}>{\sqrt {3}}.}$

Polyhedra with hexagons [edit]

There is no Ideal solid made of only regular hexagons, because the hexagons tessellate, not assuasive the consequence to "fold up". The Archimedean solids with some hexagonal faces are the truncated tetrahedron, truncated octahedron, truncated icosahedron (of soccer ball and fullerene fame), truncated cuboctahedron and the truncated icosidodecahedron. These hexagons can be considered truncated triangles, with Coxeter diagrams of the form and .

Hexagons in Archimedean solids
Tetrahedral	Octahedral		Icosahedral
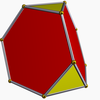truncated tetrahedron	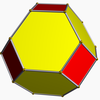truncated octahedron	truncated cuboctahedron	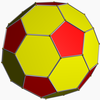truncated icosahedron	truncated icosidodecahedron

There are other symmetry polyhedra with stretched or flattened hexagons, like these Goldberg polyhedron G(2,0):

Hexagons in Goldberg polyhedra
Tetrahedral	Octahedral	Icosahedral
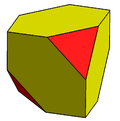Chamfered tetrahedron	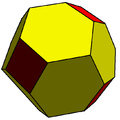Chamfered cube	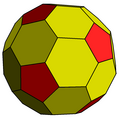Chamfered dodecahedron

In that location are too nine Johnson solids with regular hexagons:

Johnson solids with hexagons
triangular cupola	elongated triangular cupola	gyroelongated triangular cupola
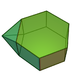augmented hexagonal prism	parabiaugmented hexagonal prism	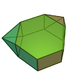metabiaugmented hexagonal prism	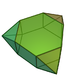triaugmented hexagonal prism
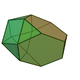augmented truncated tetrahedron	triangular hebesphenorotunda	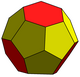Truncated triakis tetrahedron

Prismoids with hexagons
Hexagonal prism	Hexagonal antiprism	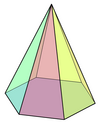Hexagonal pyramid

Tilings with regular hexagons
Regular	1-uniform
{6,iii}	r{6,3}	rr{half-dozen,3}	tr{6,three}
2-compatible tilings

Gallery of natural and artificial hexagons [edit]

• 

  The ideal crystalline structure of graphene is a hexagonal grid.

• 

  Assembled E-ELT mirror segments

• 

• 

  Micrograph of a snowflake

• 

  Hexagonal club of bubbling in a cream.

• 

  Metropolitan France has a vaguely hexagonal shape. In French, 50'Hexagone refers to the European mainland of France.

• 

  Hexagonal barn

• 

• 

  Pavilion in the Taiwan Botanical Gardens

• 

Encounter too [edit]

• 24-prison cell: a four-dimensional figure which, similar the hexagon, has orthoplex facets, is self-dual and tessellates Euclidean space
• Hexagonal crystal system
• Hexagonal number
• Hexagonal tiling: a regular tiling of hexagons in a plane
• Hexagram: vi-sided star inside a regular hexagon
• Unicursal hexagram: unmarried path, six-sided star, within a hexagon
• Honeycomb theorize
• Havannah: abstract board game played on a six-sided hexagonal grid

References [edit]

1. ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN9780521098595, archived from the original on 2016-01-02, retrieved 2015-11-06 .
2. ^ ^{a b} Meskhishvili, Mamuka (2020). "Circadian Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. eleven: 335–355. arXiv:2010.12340.
3. ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-one-56881-220-v (Chapter xx, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
4. ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
5. ^ Cartensen, Jens, "Nigh hexagons", Mathematical Spectrum 33(ii) (2000–2001), 37–40.
6. ^ Dergiades, Nikolaos (2014). "Dao'due south theorem on six circumcenters associated with a cyclic hexagon". Forum Geometricorum. 14: 243–246. Archived from the original on 2014-12-05. Retrieved 2014-11-17 .
7. ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publications, 2007 (orig. 1960).
8. ^ Gutierrez, Antonio, "Hexagon, Inscribed Circumvolve, Tangent, Semiperimeter", [1] Archived 2012-05-11 at the Wayback Machine, Accessed 2012-04-17.
9. ^ Dao Thanh Oai (2015). "Equilateral triangles and Kiepert perspectors in complex numbers". Forum Geometricorum. 15: 105–114. Archived from the original on 2015-07-05. Retrieved 2015-04-12 .
10. ^ Inequalities proposed in "Crux Mathematicorum", [2] Archived 2017-08-xxx at the Wayback Machine.

External links [edit]

Wait up hexagon in Wiktionary, the costless dictionary.

• Weisstein, Eric W. "Hexagon". MathWorld.

• Definition and properties of a hexagon with interactive animation and structure with compass and straightedge.
• An Introduction to Hexagonal Geometry on Hexnet a website devoted to hexagon mathematics.
• Hexagons are the Bestagons an animated youtube video about hexagons

v t e Cardinal convex regular and uniform polytopes in dimensions two–10
Family	A n	B north	I 2(p) / D n	Eastward 6 / Eastward seven / E 8 / F four / G 2	Hn
Regular polygon	Triangle	Foursquare	p-gon	Hexagon	Pentagon
Compatible polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-prison cell • Tesseract	Demitesseract	24-cell	120-jail cell • 600-cell
Uniform 5-polytope	v-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	half dozen-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • seven-cube	7-demicube	132 • 231 • 321
Uniform eight-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	one42 • 241 • 421
Uniform 9-polytope	nine-simplex	9-orthoplex • nine-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • ten-cube	ten-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	north-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Angle For 6 Sided Box,

Source: https://en.wikipedia.org/wiki/Hexagon

Posted by: haylessairse.blogspot.com

Share this post